Dimensionality Reduction

Linear Discriminant Analysis

Theory

LDA is a supervised dimensionality reduction technique that finds linear combinations of features that best separate classes. Unlike PCA which maximizes variance, LDA maximizes class separability.

Visualization

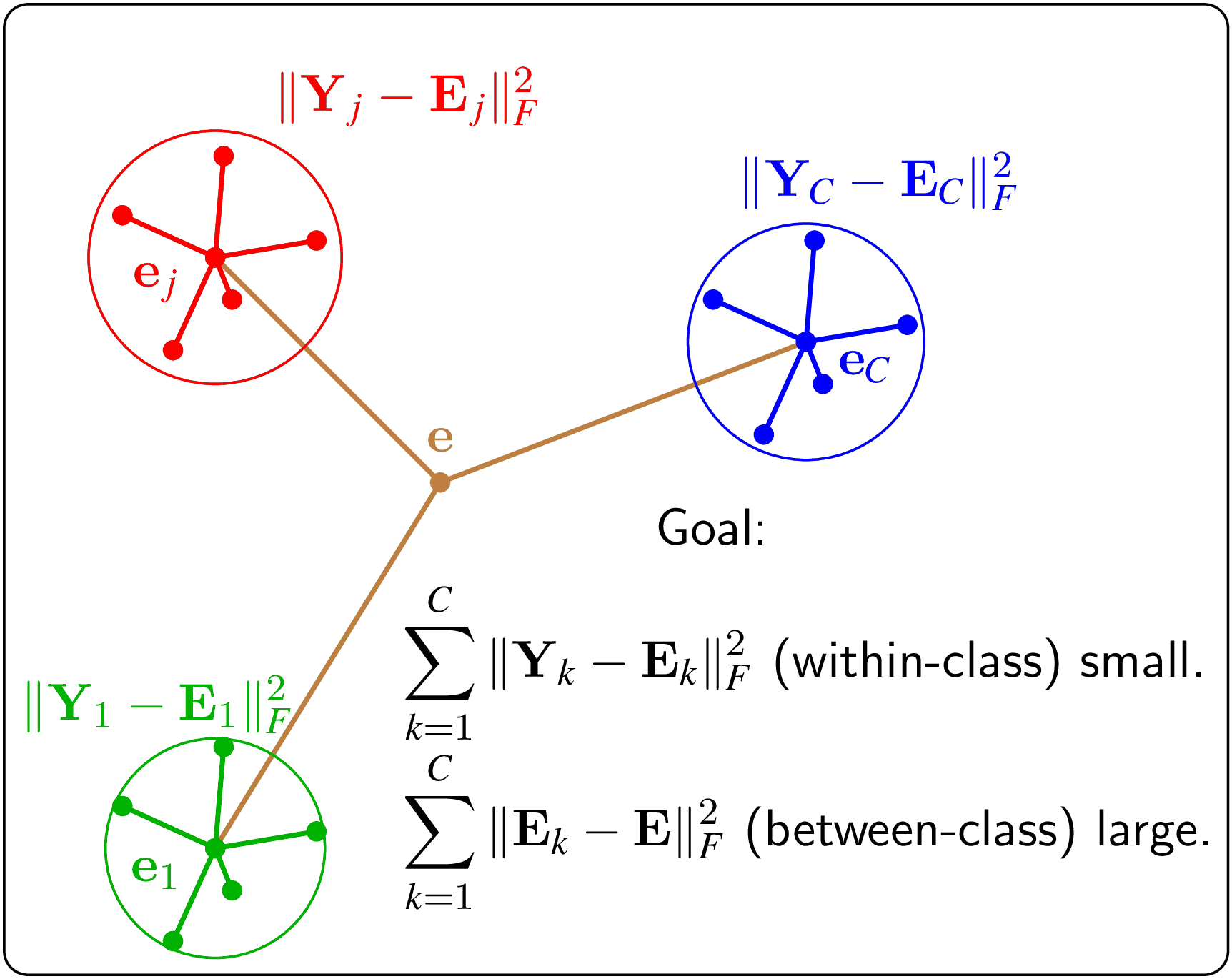
Mathematical Formulation

Objective:
maximize J(w) = (wᵀSʙw) / (wᵀSᴡw)

where:
• Sʙ = between-class scatter matrix
• Sᴡ = within-class scatter matrix

Key Difference from PCA:
• PCA: Unsupervised, maximizes variance
• LDA: Supervised, maximizes class separation

Code Example

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

# Load dataset
iris = load_iris()
X = iris.data
y = iris.target

print(f"Dataset shape: {X.shape}")
print(f"Classes: {np.unique(y)}")

# Standardize
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# Apply LDA
lda = LinearDiscriminantAnalysis(n_components=2)
X_lda = lda.fit_transform(X_scaled, y)

print(f"\nLDA transformed shape: {X_lda.shape}")
print(f"Explained variance ratio: {lda.explained_variance_ratio_}")

# Compare with PCA
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)

print(f"\nPCA explained variance: {pca.explained_variance_ratio_}")
print(f"LDA explained variance: {lda.explained_variance_ratio_}")

# LDA as classifier
X_train, X_test, y_train, y_test = train_test_split(
    X_scaled, y, test_size=0.3, random_state=42
)

lda_clf = LinearDiscriminantAnalysis()
lda_clf.fit(X_train, y_train)

train_score = lda_clf.score(X_train, y_train)
test_score = lda_clf.score(X_test, y_test)

print(f"\nLDA Classifier:")
print(f"Training accuracy: {train_score:.3f}")
print(f"Test accuracy: {test_score:.3f}")

PCA (2/2)