Optimization

Overfitting

Theory

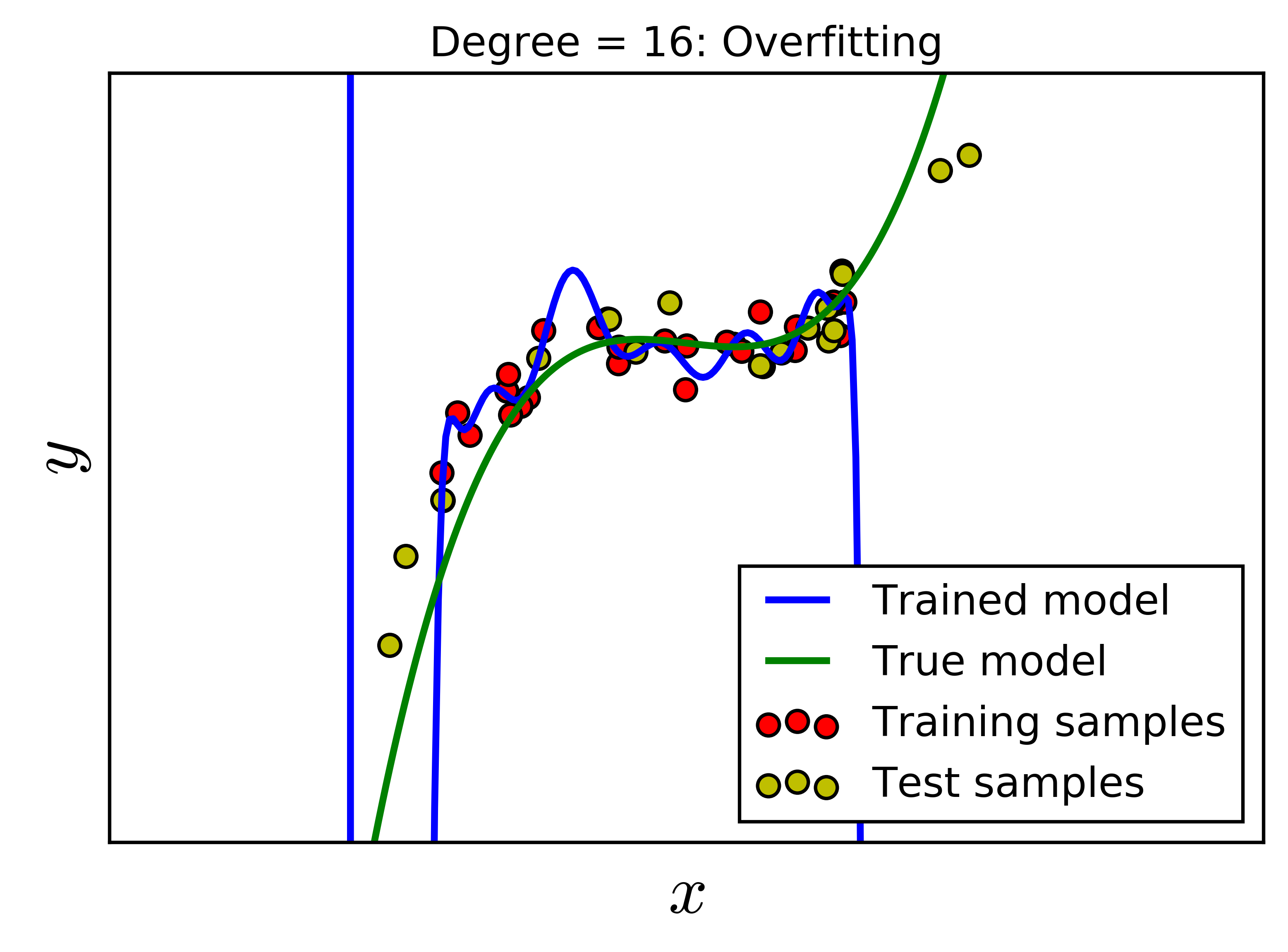
Overfitting occurs when a model learns the training data too well, including its noise and peculiarities, leading to poor performance on unseen data. The model essentially memorizes the training data instead of learning generalizable patterns.

Visualization

Mathematical Formulation

Signs of Overfitting:
• High training accuracy, low test accuracy
• Large gap between training/validation loss
• Model too complex for data size

Prevention Techniques:
• Regularization (L1, L2)
• Cross-validation
• Early stopping
• Dropout
• Data augmentation
• Reduce model complexity

Code Example

from sklearn.linear_model import Ridge, Lasso
from sklearn.model_selection import cross_val_score

# L2 Regularization (Ridge)
ridge = Ridge(alpha=1.0)
ridge.fit(X_train, y_train)

# L1 Regularization (Lasso)
lasso = Lasso(alpha=0.1)
lasso.fit(X_train, y_train)

# Cross-validation to detect overfitting
from sklearn.linear_model import LinearRegression
model = LinearRegression()
cv_scores = cross_val_score(model, X, y, cv=5,
                            scoring='neg_mean_squared_error')

print(f"CV Scores: {-cv_scores}")
print(f"Mean CV MSE: {-cv_scores.mean():.3f}")
print(f"Std: {cv_scores.std():.3f}")

# Compare regularized vs non-regularized
print(f"\nRidge Test Score: {ridge.score(X_test, y_test):.3f}")
print(f"Lasso Test Score: {lasso.score(X_test, y_test):.3f}")

MLP & Backpropagation

Convex Sets & Functions