Dimensionality Reduction

Principal Component Analysis (2/2)

Theory

Advanced PCA applications include kernel PCA for non-linear dimensionality reduction, incremental PCA for large datasets, and sparse PCA for interpretable components. Choosing the number of components can be done via variance threshold, elbow method, or cross-validation.

Visualization

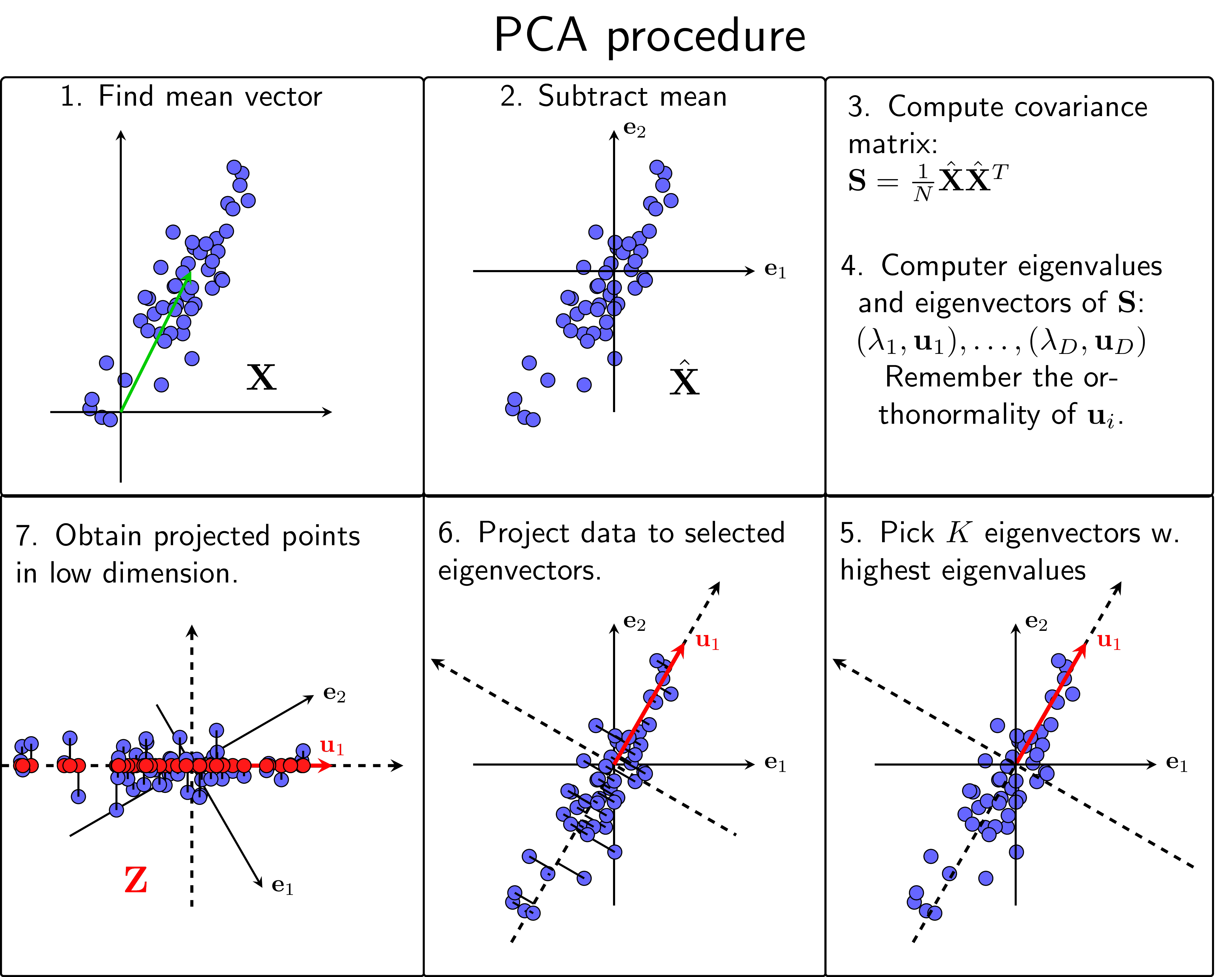
Mathematical Formulation

Choosing # Components:
• Variance threshold: Keep 95% variance
• Elbow method: Look for "elbow" in scree plot
• Cross-validation: Optimize for task

Kernel PCA:
K(x, y) = φ(x)·φ(y)

Whitening:
Transform to mean=0, covariance=I

Code Example

from sklearn.decomposition import PCA, KernelPCA
from sklearn.datasets import load_digits, make_moons

# 1. PCA for visualization (high-dim to 2D)
digits = load_digits()
X = digits.data
y = digits.target

pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)

print(f"Digits: {X.shape} -> {X_pca.shape}")
print(f"Variance explained: {pca.explained_variance_ratio_}")

# 2. Kernel PCA for non-linear data
X_moons, y_moons = make_moons(n_samples=300, noise=0.1, 
                              random_state=42)

# Linear PCA
pca_linear = PCA(n_components=1)
X_pca_linear = pca_linear.fit_transform(X_moons)

# Kernel PCA (RBF)
kpca_rbf = KernelPCA(n_components=1, kernel='rbf', gamma=10)
X_kpca = kpca_rbf.fit_transform(X_moons)

print(f"\nMoons dataset:")
print(f"Linear PCA shape: {X_pca_linear.shape}")
print(f"Kernel PCA shape: {X_kpca.shape}")

# 3. Whitening
pca_whiten = PCA(n_components=20, whiten=True)
X_whitened = pca_whiten.fit_transform(X)

print(f"\nWhitened data:")
print(f"Mean: {X_whitened.mean(axis=0)[:5]}")
print(f"Std: {X_whitened.std(axis=0)[:5]}")

# 4. Optimal # components
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_val_score

scores = []
for n in [5, 10, 20, 30, 40]:
    pca_temp = PCA(n_components=n)
    X_reduced = pca_temp.fit_transform(X)
    clf = LogisticRegression(max_iter=1000)
    score = cross_val_score(clf, X_reduced, y, cv=5).mean()
    scores.append(score)
    print(f"n={n:2d}: CV accuracy={score:.4f}")

PCA (1/2)

Linear Discriminant Analysis