SVM

Soft Margin SVM

Theory

Soft Margin SVM allows some misclassifications to handle non-linearly separable data and improve generalization. The C parameter controls the trade-off between margin size and classification errors.

Visualization

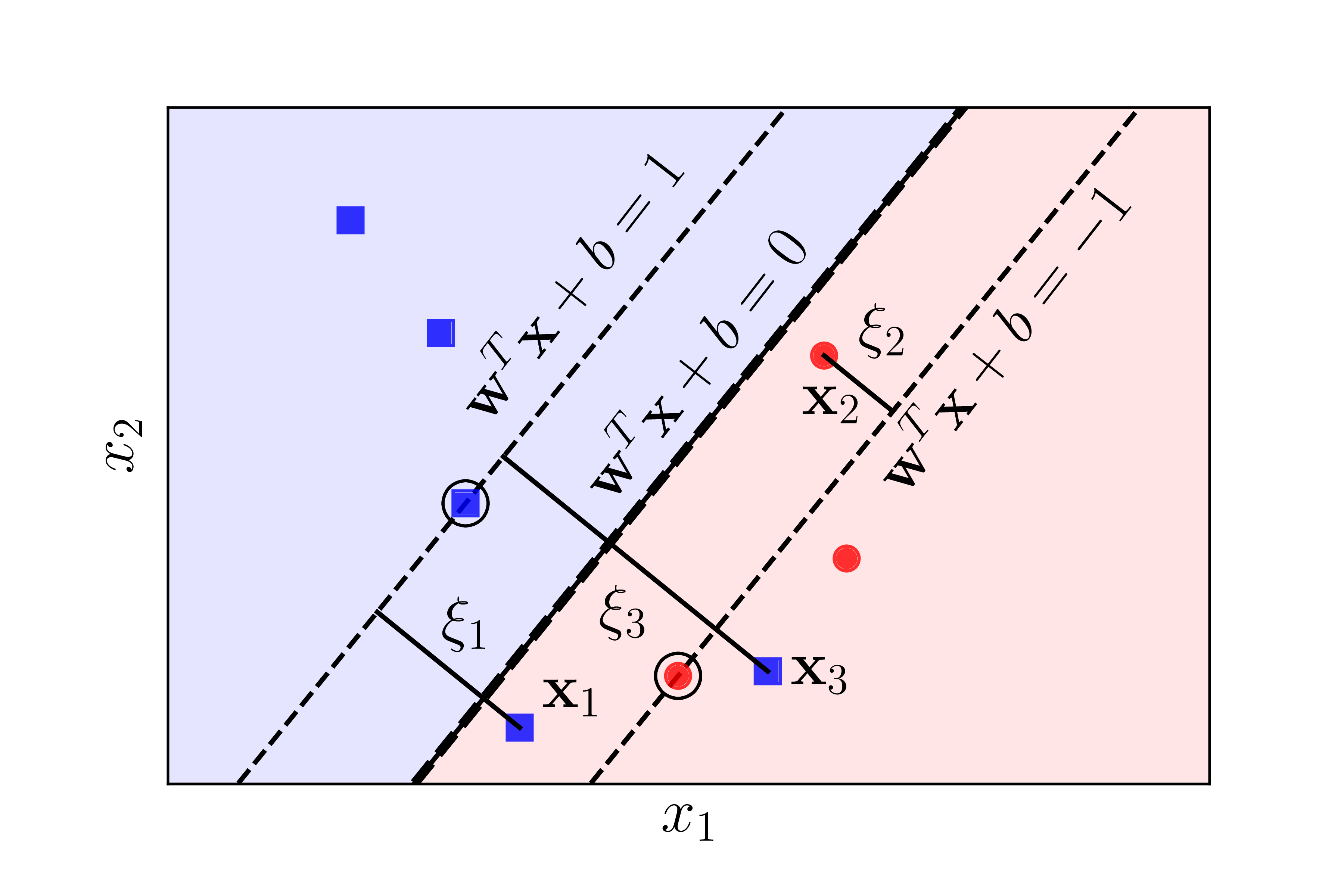
Mathematical Formulation

Formulation:
minimize ½||w||² + C·Σξᵢ
subject to yᵢ(w·xᵢ + b) ≥ 1 - ξᵢ, ξᵢ ≥ 0

C Parameter:
• Large C: Hard margin (fewer violations)
• Small C: Soft margin (more violations)

Hinge Loss:
max(0, 1 - yᵢ(w·xᵢ + b))

Code Example

from sklearn import svm
from sklearn.datasets import make_classification
import numpy as np

# Generate non-linearly separable data
X, y = make_classification(n_samples=200, n_features=2,
                          n_redundant=0, flip_y=0.1,
                          random_state=42)
y = np.where(y == 0, -1, 1)

# Train SVMs with different C values
C_values = [0.1, 1, 10, 100]

for C in C_values:
    clf = svm.SVC(kernel='linear', C=C)
    clf.fit(X, y)
    
    accuracy = clf.score(X, y)
    n_sv = len(clf.support_vectors_)
    
    print(f"C={C:5.1f}: Accuracy={accuracy:.3f}, "
          f"Support Vectors={n_sv}")

# Demonstrate trade-off
print("\nSmall C: More violations, simpler model")
print("Large C: Fewer violations, complex model")

Support Vector Machine

Kernel SVM